Climb gradient has nothing to do with speed. Let me repeat – nothing to do with speed. If speed is concerned, then we are talking about the rate of climb…

Onto our topic, we usually speak of climb gradient in the context of clearing ominous obstacles, lurking somewhere in line with your take off path. Gradient involves geometry, and most airfields that have pesky tall buildings, or mountains (as an example) in line with their runways, will usually publish a gradient for various classes of aeroplanes. These climb gradients, are established to ensure safe take offs, and the clearance of obstacles with a healthy margin.

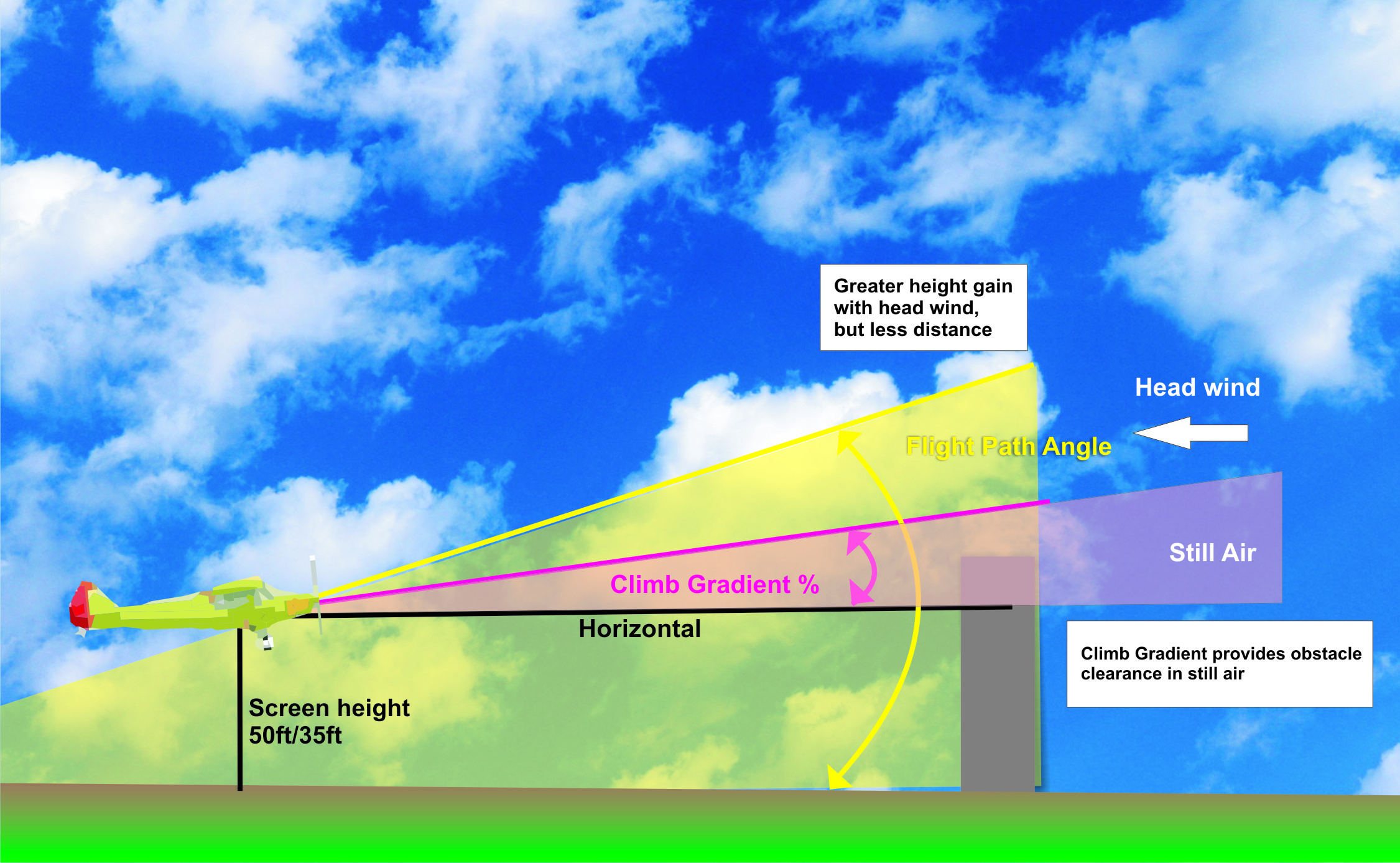
Climb gradient is essentially how steeply (the pitch angle) that an aircraft climbs, from it’s starting point, which is usually the screen height of 50ft or 35ft depending on the performance class, to the required altitude, safely clearing any obstacles. Climb gradient is the increase of altitude to horizontal air distance expressed as a percentage. Airport specified minimum climb gradients are devised based on normal operations, and do not take into account an engine failure. The most important factor in maintaining climb gradient, is determining how much the aircraft can weigh on take off, and still be able to maintain this gradient. The aircraft published MTOM (Maximum Take Off Mass) is a structural limitation, and the performance limitation needs to be accurately calculated in order to determine how much the aircraft can weigh, on a particular day, with particular conditions, in order to maintain the safe gradient. Most company operations will calculate the maximum weight, based on the loss of an engine after V1 (take off decision speed), that will still allow the aircraft to climb at the safe gradient. In smaller operations, you may have to work out the required gradient yourself, and then use the aircraft performance graphs to determine a safe take off mass.

TO CALCULATE THE STILL AIR CLIMB GRADIENT:

Still air climb gradient % = (Change in height x 100) / Horizontal distance

• The change in height refers to the difference between your starting point (be careful here to check if your screen height of 50ft or 35ft has been included or not), and the altitude at which obstacles are safely cleared.
• Horizontal distance is the ground distance to the obstacle.
• Multiply by 100 to get the gradient in percentage.

If you are missing either a vertical component (height) or a horizontal component, then this formula can be manipulated as follows:

Horizontal distance = (Vertical (height / Gradient) x 100

Vertical  = (Gradient x Horizontal) / 100

Ok, so now we have a still air gradient, but what happens if there is wind? Remember, that the gradient of climb is the ratio of the increase of altitude to horizontal distance through the air, not over the ground. If there is wind, be it a headwind or tailwind,  it makes no difference to your climb gradient because you are moving relative to the air mass. However, if we want to clear an obstacle then we do need to take into account the wind, as the wind does affect the angle along the flight track, in other words, the flight path angle which is relative to the ground.

This brings us to the second part, which is, what exactly is the flight path angle?

In order to obtain a specific climb gradient then we need hold the aircraft at a certain pitch. However, if we are considering where the aircraft is going (the trajectory) relative to the ground, then we are referring to the flight path angle. In this case, if we are looking at obstacle clearance, then wind does play a part – if there is a headwind we will have a steeper angle, and cover less ground distance,  and if there is a tailwind there will be a shallower angle, but we will cover more ground distance. So clearly the wind effective gradient is different to climb gradient, and it is this that gives the flight path angle. In order to clear obstacles it is important to calculate the effect of wind on the flight path angle, as you may not always be able to take off into a nice steady headwind – some aerodromes may have uni-directional runways which might mean taking off with a tailwind. So how do you work this out?

HOW TO CALCULATE FLIGHT PATH ANGLE

Flight Path Angle = Still air climb gradient x TAS / GS

To work out your ground speed (GS) either subtract your headwind component from your TAS, or add the tail wind component to the TAS.

Image: asisbiz.com