Well, for some of you, it is necessary to be able to calculate the distance and time from co-ordinates for exam purposes. For the rest of you, who rely on that magnificent invention called GPS, quite frankly, I don’t blame you, but it is useful to use your grey matter, and know how to work it out the old fashioned way, just in case…

To start with, you are going to need the co-ordinates of your starting point and your destination point.

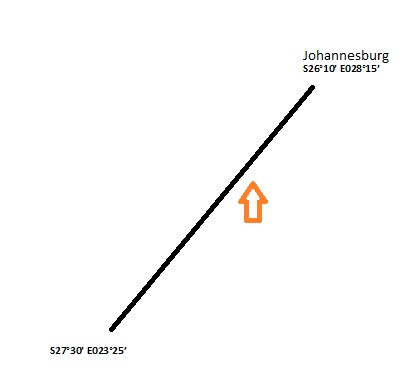
Say we want to get to Johannesburg (which lies at S26°10’ E028°15’) from a position at S27°30’ E023°25’, and we want to know how far this is, the first place to start is by drawing a sketch so that we have an idea of the direction in which we are going.

We are currently at latitude S27°30’, and we want to go to a latitude which is closer to the Equator (which is 0°), so this means that we will be traveling north. Then, if we consider our longitude, our starting point is closer to the Greenwich meridian, and our destination longitude is further east, therefore we need to travel to the right, as northwards.

Given that this is not a very long trip, we don’t have multiple changes of latitude, and the latitudes are not very high, it makes sense to fly a Rhumb line. Closer to the poles, where the convergence of the meridians is more significant, it makes more sense to fly a Great Circle track, which will provide a shorter distance, and less fuel consumption, in the case of airline operations. However, flying a Rhumb line would make our flight easier, as we would fly a constant bearing towards our destination, as a Rhumb line track cuts all the meridians at exactly the same angle.

Distance is easily calculated using the departure formula:

DEPARTURE = (dlong x 60) x COS Mean Latitude

Firstly, calculate the difference of the longitudes, and convert the minutes to decimal:

E028°15’ – E023°25’ = 4°50’
Convert 50’ into decimal 50/60 = 0.8, giving a difference in longitude of 4.8

Now, because we have two different latitudes, we need to base our calculation on the average of the two, so:
S27°30’ – S26°10’ = S26°48’ (remember to convert minutes to decimal = 26.8)

The completed formula will look like this:

DEPARTURE = (4.8 x 60) x COS 26.8
                       = 257NM

Now that we have the distance, we can calculate the time it will take us to get to Johannesburg. In order to get time, we use this formula:

Time = Distance/Speed

When using speed, it is important to factor in the wind, as this will make us either arrive faster or slower. In order to calculate the groundspeed, we will need to know the wind direction and speed (obtainable from the local ATIS). If our airspeed is averaging around 90kts, and we have determined that we have a 10kt tailwind, then we will be faster, so ADD this to the 90kts. We are now traveling over the ground at 100kts.

Using the formula:

Time = 257 / 100
          = 2.57 (Convert 0.57 to minutes by x60)
          = 2h34’

So as you can see, it is really not that challenging! These calculations can be really useful for determining if you have sufficient fuel, and also providing estimated time arrival. Go on, give it a try…